Pool¶
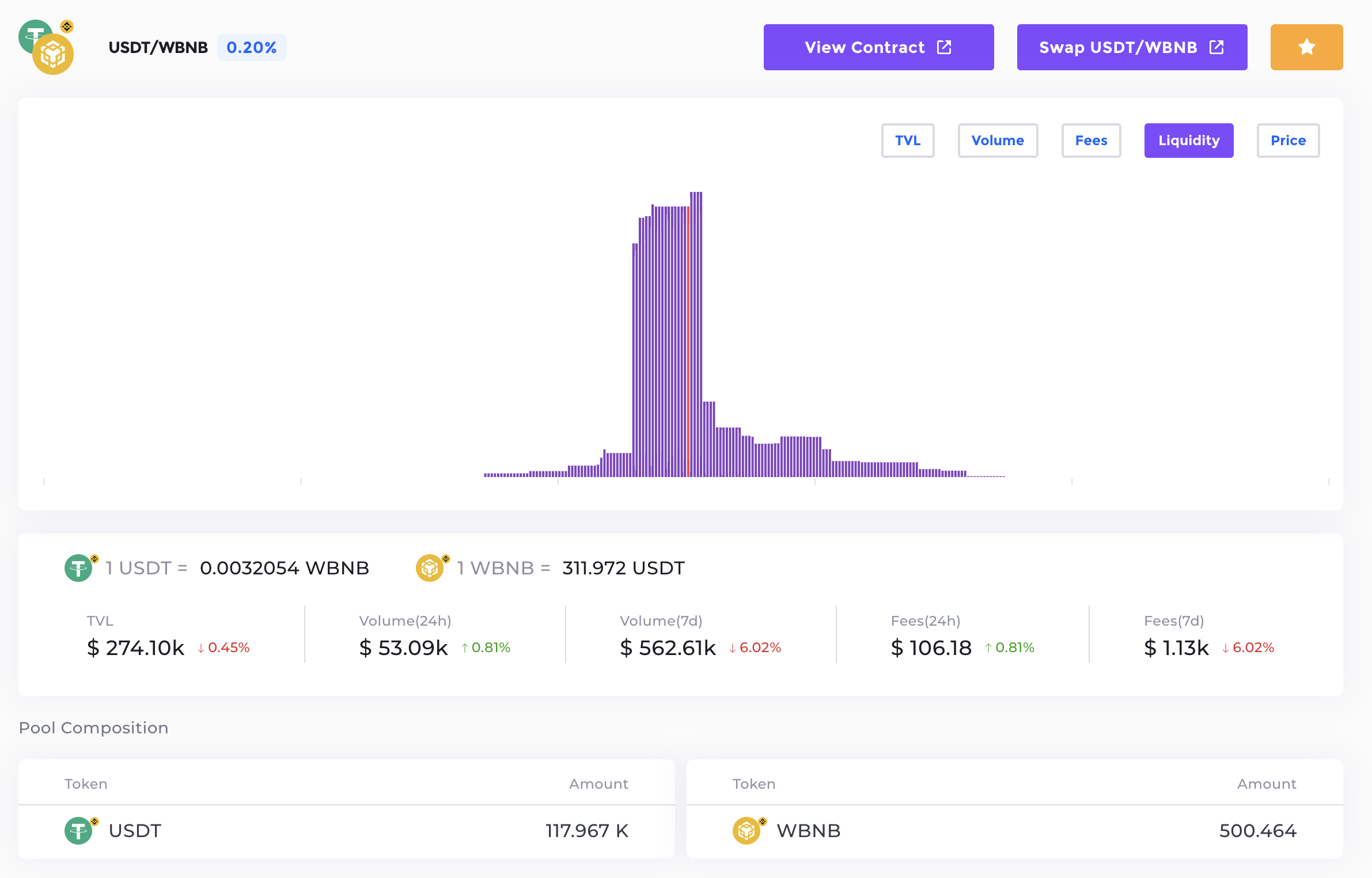
An example of iZiSwap pool status.¶
A POOL in iZiSwap is distinguished with tuple <tokenA, tokenB, fee>, e.g., <BNB, USDT, 2000> means the pool with token ETH and USDT with fee rate 0.2%, where fee means the transaction fee a trader will pay if he initiate a swap action. tokenA and tokenB are tokens that must implement the ERC-20 standard.
A pool is similar to a trading market in CEX. For example, if you want to trade BNB and USDT on Binance, you go to the BNB-USDT spot market, while here you interact with the <BNB,USDT,2000> pools. Liquidity are added into it and organized in a certain structure, with the help of the following design.
Point¶
A POINT is a price point p, which means 1 tokenA = p tokenB. The price space is discrete in our design:
We choose \(d=0.0001, p_0 = 1\) and \(i \in (-799999, +799999)\) in our current implementation. We also call Point as Tick and make no distinction between these two terms.
Price discretization is the starting point of our protocol’s design and serves as the first perspective to describe DEX behavior. In contrast, UniswapV3’s starting point is the function curve relationship between the reserves of two tokens, which then derives the concept of price. Therefore, in comparison, iZiSwap is clearer in defining prices by starting from the concept of price itself.
Liquidity¶
LIQUIDITY can only be put on the discrete points above, and itself is a measurement of how many tokens are putted. The liquidity we define needs to satisfy symmetry, thereby eliminating logical differences between the two tokens and allowing for a time-efficient management solution. Taking all factors into consideration, the liquidity definition in iZiSwap is as follows:
where \(L_i\) represents the liquidity quantity on price point \(p_i\), \(x,y\) are the quantities of tokenX and tokenY respectively.
As illustrated in the figure, the height of the purple bars represents the amount of liquidity at different price points. It is important to note that for liquidity at different price points, even if their sizes are the same, the number of tokens they contain is not the same because \(p_i\) is different. However, the difference between them is minimal at adjacent \(p_i\) points.
Here, when we refer to liquidity, we are primarily referring to the conventional liquidity used in Automated Market Makers (AMMs). This means that when the price repeatedly crosses a certain price point, the liquidity above that price point repeatedly acts as the counterparty in trades. Later, we will discuss limit orders. Unlike conventional liquidity, once limit orders at a specific price point are filled, they no longer act as counterparties in the opposite direction. In this sense, limit orders can be seen as one-time liquidity.
Pool Status¶
The STATUS of a pool mainly records the current price and the liquidity on each price point. As illustrated in the figure, the red line refers to the current price and the liquidity on it.
As the trades progress, the current price will move back and forth. This happens only when the liquidity at the current price point is exhausted. At the current price point, both tokens may be present, while on either side of the price point, only one token will be available.